Методы исследования безопасности трудас помощью функциональной сети GERT

Последняя, в свою очередь, может изменяться в результате воздействия на нее со стороны двух первых компонентов исследуемой системы, а степень такого изменения значительно определяется принятой технологией работ.

Таким образом, подтверждается необходимость представления исследуемого объекта как сложной человекомашинной системы.

Важное место в исследовании безопасности принадлежит формализации и моделированию различных аспектов. Моделирование является основным методом исследований во всех областях знаний и научно обоснованным методом оценок характеристик сложных систем, используемых для принятия решений в различных сферах инженерной деятельности, в том числе и в области обеспечения безопасности технологических процессов.

Главные требования к моделированию процессов в человекомашинной системе заключаются в необходимости учета их особенностей и цели исследования. Применительно к безопасности, они должны состоять в следующем: системность (учет лишь наиболее существенных факторов аварийности и травматизма), сочетание возможностей описания и оценивания их характеристик, использование таких языков моделирования и алгоритмов, которые – не велики по алфавиту, но в то же время достаточны для семантического представления исследуемых категорий. Желательно, чтобы они были доступны, по возможности, как заказчику, так и пользователю, а также пригодны для средств электронно-вычислительной техники.

Наиболее удовлетворяющими данным требованиям могут являться модели, представляющие процесс появления отдельных предпосылок и развития их в причинную цепь происшествия в виде соответствующих диаграмм причинно-следственных связей – диаграмм влияния.

В последние годы интенсивно разрабатываются диаграммы влияния из класса семантических или функциональных сетей, которые являются графами, но с дополнительной информацией, содержащейся в их узлах и дугах (ребрах). Из них наиболее пригодны для исследования возникновения и предупреждения происшествий, так называемые функциональные сети типа PERT и GERT.

Достоинства таких сетей – возможность объединения логических и графических способов представления исследуемых процессов, учет стохастичности информации, выраженной узлами и дугами, доступность для моделирования циклических и многократно наблюдаемых событий, наибольшие (по сравнению с другими типами диаграмм, например, дерево событий, дерево отказов) логические возможности – в смысле строгости, компактности и простоты корректировки условий наблюдения моделируемых событий и процессов [1].

Функциональные сети GERT и их модификации обладают стохастической структурой, что достигается присвоения узлам логических функций, а связям между ними – случайности их реализации, активности или соблюдения другого условия [2]. Для завершения исследуемого процесса или появления интересующего события необходимо реализовать определенную совокупность узлов и дуг, достаточную для их наблюдения. В тех случаях, когда требуемый для перехода ресурс является случайной величиной, каждая конкретная реализация сопровождается выбором его нового значения – в соответствии с заданным конкретной связью вероятностным или возможностным распределениями.

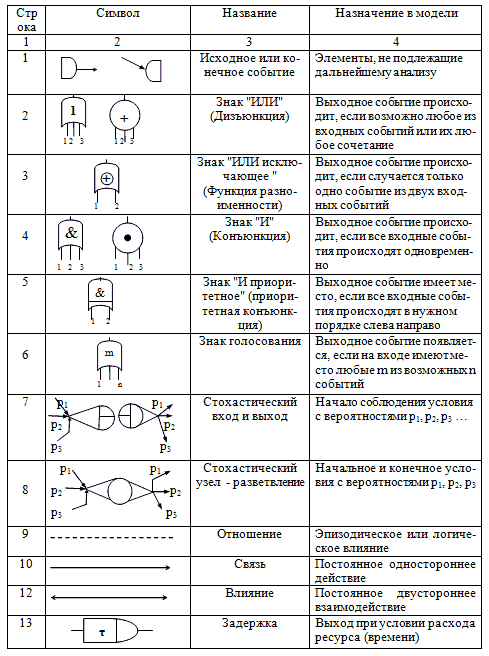
Сети GERT имеют в общем случае четыре типа узлов (источник, сток, метка и статистика), каждая пара которых является ориентированной ветвью с определенным числом степеней свободы. Характеристики символов, используемых в диаграммах сети GERT, приведены в таблице 1.

В отличие от графов и деревьев, узлы сети GERT могут характеризоваться числом степеней свободы, которые обычно указывают на количество непосредственно им предшествующих (инцидентных) условий, необходимых для реализации конкретного узла.

С целью пояснения одного из возможных принципов статистического и имитационного моделирования процесса возникновения происшествия приведем пример реального события, происшедшего в НГЧ – 4 Свердловск – пассажирский.

23.11.01 года слесарь этой организации - 46 лет, стаж работы по профессии 2 года, при устранении аварии на теплотрассе в подвале дома смертельно травмирован электротоком. Обстоятельства случая следующие, слесарь попытался включить освещение подвала и оказался под напряжением в результате плохой изоляции электропроводки. При этом слесарь стоял на полу, залитым водой. Работы производились в одно лицо.

В результате проведенного анализа можно выделить следующие основные причины, приведшие к электротравме: неправильные действия обслуживающего персонала, которые связаны с недостаточной обученностью, нарушением технологии безопасного ведения работ – работал в одно лицо, неудовлетворительным проведением инструктажа перед выполнением работ в помещениях особоопасных; отсутствие контроля изоляции электрооборудования в подвале; применение для питания электрооборудования в подвале напряжения 220 В вместо допустимых, в данном случае, 12 В.

В этом случае диаграмма причинно-следственных связей будет выглядеть следующим образом:

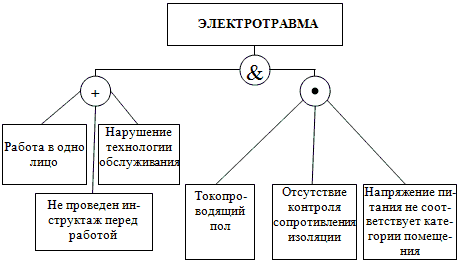
Рисунок 1 – Причинно-следственная связь электротравмы

Сеть GERT выглядит следующим образом:

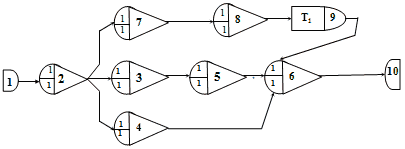
Рисунок 2 – Сеть стохастической структуры электротравмы.

Дуги данной сети обозначают следующие ситуации:

1-2 – Работник вошел в помещение с аварийным состоянием электрооборудования;
2-3 – Напряжение в сети освещения помещения 220 В;
2-4 – Напряжение в сети освещения помещения 12 В;
2-7 – Работа производится без инструктажа и допуска;
3-5 – В сети освещения нарушена изоляция;
5-6 – Присутствие токопроводящего пола (пол залит водой);
6-10 – Устройство защитного отключения не срабатывает;
7-8 – Работа производится в одно лицо;
8-6 – Обращение к неисправному электрооборудованию;
4-6 – Фактор опасного воздействия электрического тока отсутствует.

Для определения вероятности наступления конкретного события сети – Q, математического ожидания – M[T] и дисперсии времени до его появления – D[T], проведем упрощение исходной модели, путем объединения последовательных и параллельных контуров в единственную ветвь с эквивалентными исходными параметрами P_ij, M_ij(S) и их преобразованием W_ij*(S) – коэффициентом пропускания динамической системы.

Общее выражение для передаточной функции сети будет иметь следующий вид:

где a – количество минимальных пропускных сочетаний внутри графа;
D_i – число дуг, соединяющих узлы графа в i-ом сочетании;
P_ij – вероятность передачи сигнала (перехода индикатора) между j-ми дугами графа в конкретных i-ых сочетаниях.

Для расчета вероятности появления происшествий установим все пропускные сочетания:{1.2.3.5.6.10}, {1.2.4.6.10}, {1.2.7.8.9.6.10}. Если проанализировать все возможные ситуации в нашем случае и задаться вероятностями событий, то выражение для передаточной функции графа (коэффициента пропускания сети GERT) можно выразить через формулу:

Q=W_E(S)_S=0=P₁₂.P₂₃.P₃₅.P₅₆.P₆₁₀ + P₁₂.P₂₄.P₄₆.P₆₁₀ + P₁₂.P₂₇.P₇₈.P₈₉.P₉₆. P₆₁₀

Значение математического ожидания времени возникновения аварийной ситуации и его дисперсию находим из первой и второй производных выше приведенной формулы:

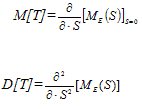
Вероятности событий, связанных с действием человека-оператора и надежностью работы технических устройств, в том числе и защитных средств в электроустановках, можно взять из специальных справочников. Полученные расчеты позволят в дальнейшем моделировать аналогичные и более сложные случаи взаимодействия в человеко-машинной системе

Литература:

1. Ахьюджа Х. Сетевые методы управления в проектировании и производстве/ Пер. с англ.- М.: Мир, 1979. – 640 с.
2. Prisker A. Modelling and analisis using Q-GERT networks // J.Willey & sons. 1977/ - 312 p.
3. Питерсон Дж. Теория сетей Петри и моделирование систем // пер. с англ. – М.: Мир, 1984. – 264 с.

Павлов В.В. старший преподаватель каф. БЖД, УрГУПС